The Astronomy of Houses

Introduction

There is general agreement amongst astrologers about the signs and what they signify, and how to define in which sign a planet is located, except possibly for the dispute between using tropical or sidereal signs. Houses are much more controversial. There are many different ways to define the location of the house cusps, and so to determine in which house a planet is located.

The houses of a chart serve two functions. On the one hand, they denote areas of life, and on the other, they determine the strength of a planet (planets in angular houses: 1st, 4th, 7th and 10th, are stronger than those in succedent or cadent houses). Our understanding of the area of life corresponding to each house has changed over time, so the traditional descriptions found in Lilly [1], or Houlding's recent book [2] differ in some respects from descriptions based on 20th century ideas [3, 4, 5]. However, this article is not concerned with house meanings, but with how we define which house a planet occupies: how we calculate the house cusps.

Planets in signs and houses operate on very different timescales. The sign a planet occupies depends on the date, with planets passing through all the signs in anything from 28 days (the Moon), to over 240 years (Pluto). The house a planet occupies depends on the time of day and location, with each planet passing through all twelve houses each day. As we will see, these very different timescales imply a very different basis for calculating a planet's sign and for calculating its house position.

Over time, many different methods of house division, or house systems, have been suggested, and a significant number of them are currently in use. Astrologers seem to have found it very difficult to decide which house system works best. Writers have pointed out the advantages of one and the deficiencies of another, but no consensus has emerged. This article will not be adding fuel to that debate! My aim is to suggest some reasons for different systems having been proposed in the past, and to make clear just how each system is constructed. If readers can understand how a particular system works in practice, how it relates to what is happening in the sky and the astronomy behind the house cusp calculations, they will be able to make a more reasoned choice of system for themselves. I should point out at the start that some astrologers have suggested that different house systems are appropriate for different purposes: one system for natal work, another for mundane, another for horary, etc. I will not be discussing this further but recommend the idea as worth further investigation.

In explaining how the houses are constructed, I will be using some simple diagrams, but if you are not familiar with the celestial sphere and the relationship between the ecliptic, celestial equator and horizon, before continuing with this article you may wish to read another of my articles on this website: Charts are not flat. For those interested in more detail on house construction and some of the history I recommend the excellent book by R. W. Holden [6].

House Systems

No single classification of house systems adequately covers all the many possibilities; however, following Holden's approach, we can distinguish three broad classes of house system:

• Ecliptic Systems: These divide the ecliptic itself. Some of the earliest house systems, such as Porphyry, are of this type.
• Space Systems: These divide the volume of the celestial sphere and then determine how the resulting house cusps relate to the ecliptic. Regiomontanus and Campanus houses are of this type.
• Time Systems: These divide the daily (24 hour) rotation of the Earth, and the resulting house cusps are then related to ecliptic positions. Placidus houses are of this type.

Most house systems, such as Porphyry, Campanus or Placidus, produce houses of unequal size, when measured on the ecliptic.

Another way to classify house systems is to distinguish quadrant and non-quadrant house systems. Quadrant systems divide the quarters ('quadrants') of the sky between the Ascendant, MC, Descendant and IC, treating these as the cusps of the First, Tenth, Seventh, and Fourth houses, respectively. They differ in where they place the intermediate house cusps. These quadrant systems give Angular, Succedent and Cadent houses. A planet in an Angular house, such as the first, tenth, etc. is considered stronger than one in a Succedent house, such as the second, fifth, etc., and a planet is weakest in its effects when in a Cadent house, such as the third, twelfth, sixth.

Ecliptic Systems

Whole Sign Houses

Probably the oldest house system is the Whole Sign system (not to be confused with the similar Equal House system, discussed below). This is a non-quadrant ecliptic system. James Holden, who researched early systems of house division, particularly the early Greek systems, points out [7] that the system used in the Hellenistic tradition was whole sign houses, or what he called the "sign-house" system. Robert Hand in his booklet [6] is also of the opinion that Whole Sign houses are probably the earliest system. In this system, the first house is the whole of the sign that is rising; the second house is the next sign to rise, and so on. In figure 1 (which is shown with Placidus houses), the first house is from 0 Pisces to 30 Pisces, the second house the whole of Aries and so on. If we look at Uranus, by Placidus it is in the first house, by Whole Sign, it is in the second; similarly, Jupiter is in the first by Placidus, but in the third by Whole Sign.

However, even with the Whole Sign system things are not quite that simple. Vettius Valens was a 2nd-century Hellenistic astrologer, and younger contemporary of Ptolemy. In his booklet, Hand [8] suggests that Valens used Whole Signs for determining the area of life a planet would affect, but used a quadrant system (probably Porphyry) to determine the strength of the planet. In most modern house systems, the same set of houses fulfils both functions: area of life and planetary strength.

A problem with Whole Sign houses is that the house cusps cannot easily be used for timing events. As houses correspond to signs, a transiting planet conjunct the cusp of the first house is also sextile the cusp of the third, square the cusp of the fourth, trine the fifth, etc. In addition, when a transiting planet moves from one house to the next it is, at the same time, changing sign.

Porphyry Houses

The oldest and simplest of the quadrant systems is Porphyry. The four quadrants (the areas between the angles) are each divided into three equal parts to get the cusps of the intermediate houses. So, in figure 1 above, the distance from the ascendant to the IC is 4PI54 to 20GE02, which is 90 degrees (three signs) plus 15 degrees 8 minutes, which gives 105 degrees 8 minutes. This distance is divided by three and added to the ascendant to give the second cusp: 105 degrees 8 Minutes divided by three gives 35 degrees 3 minutes (less a third of a degree, which we will ignore). Thus, the second cusp is at 4PI54 plus 35 degrees 3 minutes, which gives 9AR57. Similarly, by adding another 35 degrees 3 minutes we get 15TA00, the third house cusp. This puts Uranus in the second and Jupiter in the third.

Equal House

Like Whole Sign Houses, this is a non-quadrant ecliptic system. In both systems, each house is 30 degrees long; however, in Equal House the ascendant is the cusp of the first house. Therefore, in figure 1, the second house starts at 4AR54, the third at 4TA54, and so on. One issue with this system is that, because all the cusps are at the same degree position in each sign, transits to house cusps are in fact aspects to the Ascendant: the third cusp is sextile the ascendant, the fourth cusp square the ascendant, and so on.

The MC in Whole Sign and Equal House

Porphyry is a quadrant system, and so the tenth house cusp is the MC, but Whole Sign and Equal houses do not have the MC as the tenth cusp. Depending on the latitude, the MC can fall in the 8th, 9th, 10th, or 11th house. This is often seen as a significant problem with these non-quadrant systems. This takes us back to Valens; do we use the houses as indicators of planetary strength (as well as the area of life affected), or is strength determined by a planet's placement in relation to the angles?

Ecliptic, Equator, or Space Systems?

There are only three common ecliptic based house systems: Whole Sign, Equal House and Porphyry. It can be argued that the ecliptic is the wrong thing to use in deciding the house of a planet. The sign a planet occupies determines how the principle represented by the planet will function, while the house it occupies determines in which area of life a planet will manifest its action. To use the signs or any other ecliptic based division to determine the area of manifestation seems inconsistent. It is often argued that the signs divide the Earth's orbital plane into 12 equal segments and so by analogy, the houses should divide the Earth's rotational plane (the equator, or time), or the celestial sphere, into 12 equal segments. We will consider this later.

House Cusps

Before considering non-ecliptic based systems, I need to say something about the idea of a house cusp. The cusps have two functions. Firstly, they determine the sign ruling the house and so the house's ruling planet. Secondly, they determine the division between houses, but not necessarily the start of a house. What does that mean? In Christian Astrology [1], pages 33 and 151, Lilly refers to a 5-degree orb of influence that precedes the cusp of a house. Suppose the second house cusp is at 15 Taurus, and a planet at 11 Taurus. Lilly, and other early authors would view the planet as being in the second house, not the first. Thus, the start of a house is about 5 degrees before the cusp. The cusps determine the house divisions, but do not mark the start of each house, which is 5 degrees earlier.

This traditional view of house cusps derives from considering the cusp as the most powerful point of a house's influence.

There is a further point to consider if we allow this 5-degree orb. If we use transits (or progressions) to house cusps for timing of events, which point should we use? Is it the transit to the cusp, or the entry of the planet into the 'orb of influence' that marks the transit? This is something that would benefit from further work.

The Celestial Sphere

In order to explain the different systems of house division and how they are constructed, I will need to use diagrams of the celestial sphere and show the various great circles, such as the equator, ecliptic, horizon, etc. A diagram with them all shown, along with the construction of the houses, can be very confusing, so first I will show some simple diagrams, and then add extra information as needed.

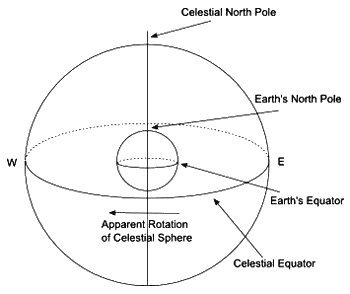
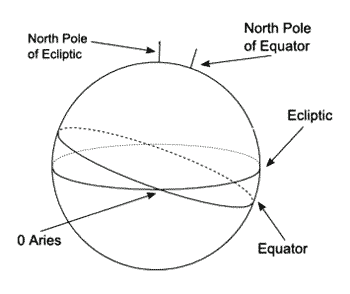
We start with the earth, showing the equator and the North Pole (Figure 2), this is then projected outwards onto the sky to form the celestial sphere. Note that the North Pole is at 90 degrees to the equator. In what follows, the point that at 90 degrees to any of the great circles will be called the pole of that circle. Just as the pole of the equator is at 90 degrees to all points on the equator, there is a pole of the ecliptic at 90 degrees to all points on the ecliptic, a pole of the horizon, and so on. This is shown in Figure 3.

Clearly, there are two poles, one above and one below the great circle, but it does not make any difference which we use in the construction of the houses. We will often use the pole of a great circle to 'project' points, usually onto the ecliptic. We want the position of the house cusps on the ecliptic.

If the cusps are generated by dividing the equator into 12 sections (as will happen in the first system we look at below), we need to take lines from one pole to the opposite pole, crossing the great circle of the equator at right angles, and note where these lines cross the ecliptic. Think of the lines of longitude on the earth, going from the north pole, across the equator and on to the south pole.

It is easy to get confused by this. Dividing a great circle, such as the celestial equator or the ecliptic and then taking lines from the pole of the circle being divided to cross it at right angles is like dividing the earth's equator and taking lines from the geographic North (or South) pole to give lines of geographic longitude. However, geographic longitude is measured on the earth's equator, whereas astronomical/astrological longitude is measured on the ecliptic.

Finally, note that often we will project from the poles of the circle being divided to get the ecliptic positions, but sometimes we will use another pole. More of that when we come to it.

Space Systems

Meridian House System

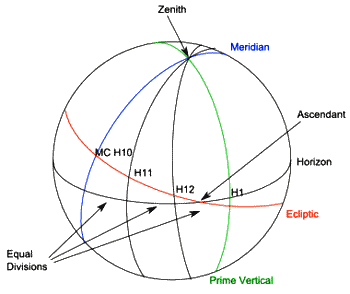
Perhaps the simplest of the space systems, the Meridian system (also known as the Axial Rotation system or the Zariel system) is based on the equal division of the celestial equator. The system was introduced in the early 20th century but has never achieved widespread popularity.

Figure 4 shows the construction of the Meridian house cusps. The diagram contains two extra great circles. The horizon is simply the local horizon projected onto the celestial sphere. Its only purpose in this diagram is to define the Ascendant, which is where the horizon intersects the ecliptic. The other is the celestial meridian which is the great circle passing through the north and south poles of the celestial equator and through the zenith at the location of the observer (directly overhead). The meridian is perpendicular to the celestial equator and the horizon. The point where the meridian crosses the ecliptic is the Mid Heaven (MC).

To create the meridian house cusps, we start where the meridian crosses the celestial equator and divide the equator into twelve 30-degree segments. These points on the celestial equator are then projected onto the ecliptic from the pole of the equator. Note, the first house cusp does not, in general, equal the ascendant, although the tenth cusp is the MC.

The Meridian house cusps do not depend on birth latitude and so there is no problem in extreme latitudes.

Meridian houses have never become generally popular; however, the system has been used by the Uranian School. Perhaps the main justification for its use is theoretical. As the signs are derived from the movement of the earth around the sun, it is argued that the houses should be based on the daily rotation of the earth on its axis, and that this is best seen in the movement of a planet in relation to the celestial equator. As the Meridian system is constructed by division of the equator and projected from the pole of the equator, it has some claim to theoretical justification. In terms of our earlier classification, this is a non-quadrant system that can be described as both space- and time-based.

Morinus House System

The Morinus system, devised by Jean Baptist Morin in the 17th century, is very similar to the Meridian system.

As with the Meridian system, we start with the local meridian where it crosses the celestial equator, and then divide the equator into twelve 30-degree sections. However, instead of projecting these celestial equator points onto the ecliptic from the pole of the equator as we did in the meridian system, we project them from the pole of the ecliptic.

This is a non-quadrant system as the tenth Morinus cusp is not the MC, and the first Morinus cusp is not the Ascendant. Note that, as with Meridian cusps, the Morinus cusps do not depend on the birth location's latitude. In addition, as we are projecting positions onto the ecliptic from the pole of the ecliptic, planetary latitude, the distance north or south of the ecliptic, has no effect. The house position of a planet depends only on its ecliptic longitude.

Regiomontanus House System

This is the first of the non-ecliptic systems we will consider that has become reasonably popular. It was introduced by Regiomontanus (Johannes Muller) in the 15th century as a modification of the Campanus system (considered next).

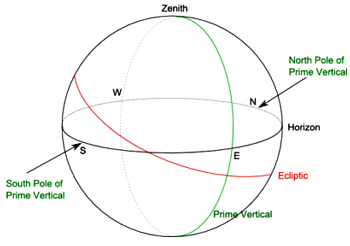
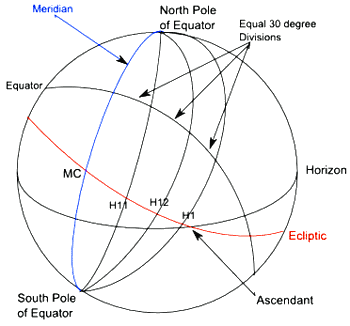
To understand its construction, we need to introduce another great circle: the prime vertical, which passes through the point on the celestial sphere directly above the observer (the zenith) and the points on the horizon due east and west of the observer (see figure 5). The poles of the prime vertical are the points on the horizon due north and south of the observer and are at 90 degrees to all the points on the prime vertical.

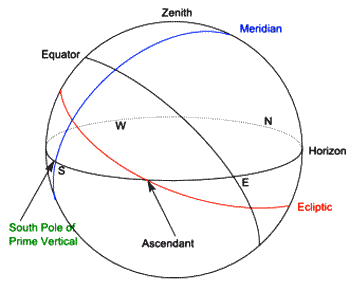
To construct the Regiomontanus house cusps we do not need the prime vertical itself, just its poles. In addition, we will once again use the Meridian and the celestial equator, as shown in figure 6.

As with the previous two house systems, we start with the equal (30 degree) division of the celestial equator (starting at the meridian) as shown in figure 7. We now project these points onto the ecliptic from the pole of the prime vertical.

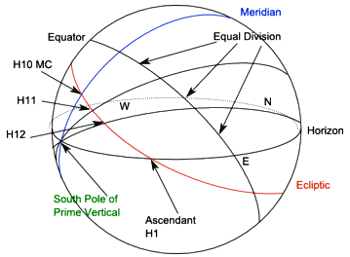
In the Meridian system we projected from the pole of the equator, in the Morinus system we projected the same points from the pole of the ecliptic, and in the Regiomontanus we project the same points from the pole of the prime vertical.

Because the meridian and the horizon are at right angles to each other, and the pole of the prime vertical is on the horizon, projecting from the pole of the prime vertical makes the MC the 10th house cusp and the ascendant the 1st house cusp. This is a great advantage over the previous two systems.

Campanus House System

The Campanus house system was introduced in the 13th century and, like Regiomontanus, has been popular at various times. It still has a significant following and Dane Rudhyar recommended the use of Campanus houses in his book The Astrology of Personality [9].

John Addey, a founder of the Urania Trust, also favoured the use of Campanus houses. To predict the winner of a horse race, he used the start of race chart and used the next planet the Campanus 5th cusp would aspect as indicating the name of the winning house [10]. This is still a popular method used by sports astrologers.

We start from figure 5 above. We again take the meridian as our starting point, and now divide the prime vertical into equal 30-degree sections. These divisions are projected from the pole of the prime vertical onto the ecliptic, as shown in figure 8.

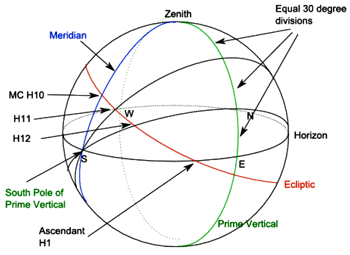
A practical advantage of Campanus houses, like Regiomontanus, is that the MC is the 10th cusp and the Ascendant the 1st cusp. Because we are equally dividing the prime vertical, and then projecting from its pole, each house contains the same volume of the celestial sphere.

There is a potential issue when constructing Campanus cusps for locations at high latitudes. As we move away from the geographic equator, the angle between the prime vertical and the ecliptic becomes larger. Within the Arctic and Antarctic circles, they can be at right angles to each other making the construction of cusps impossible. Even in less extreme latitudes, there can be a large angle between the prime vertical and the ecliptic causing very distorted houses, with their sizes on the ecliptic varying greatly.

Zenith or Horizontal House System

The final space system I will consider was introduced in the early 20th century but never achieved widespread popularity, although it is used by some North American astrologers. It has some advantages at high latitudes.

In this system, it is the horizon that is divided into equal 30-degree sections (starting at the meridian) by great circles passing through the Zenith (giving the system its name), cutting the horizon at 90 degrees and continuing to the Nadir. The house cusps are where these great circles cross the ecliptic.

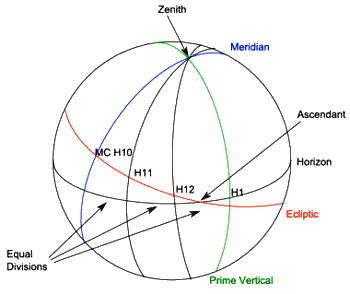
Note that, although the MC is the tenth house cusp, the cusp of the first house is not the ascendant. Where the prime vertical intersects the ecliptic is sometimes called the 'Electric Ascendant', and the ecliptic point opposite it (in the West) is called the Vertex. The Vertex is sometimes used in charts that use a different house system than the Zenith system.

There is a certain naturalness about this system. If we go outside and look at the sky, the Zenith houses are equal volumes of space around us. Each house starts at the point above our head, takes in an equal sized section of the horizon, and continues to a point directly beneath our feet. In addition, whereas the Campanus system produces distorted houses at high latitudes, the Zenith system is the reverse. The ecliptic is low down, near the horizon in high latitudes, so a system that divides the horizon does not distort the house sizes on the ecliptic. On the other hand, near the equator, the ecliptic will be nearly at right angles to the horizon, and so the Zenith houses will have very distorted house sizes.

Space Systems in Summary

Before finishing our consideration of space systems of house division we should note that only a few of the systems that are theoretically possible have ever been proposed as practical house systems, and fewer still have become popular.

To calculate the house cusps using space systems we could equally divide any of the great circles on the celestial sphere and then project these points onto the ecliptic from the pole of any of the circles. The four great circles we could divide are equator, meridian, prime vertical and horizon. (Dividing the ecliptic gives Ecliptic System houses.) These could be projected from the poles of the ecliptic, horizon, equator, prime vertical and meridian). Hence, 20 variants are possible. Because projection from the pole of the meridian produces very distorted cusps, only 16 are practical possibilities, and we have considered five. We should note that of these, three involve equal division of the equator.

Time Systems

Time systems calculate house cusps on a different basis to the space systems we have looked at above. I will discuss three systems: Alcabitius, Placidus and Koch. They all use the concept of "trisecting a semiarc". The meaning of trisecting is simple enough: dividing something into three equal parts. A semiarc is the apparent movement of a specific point between the angles. Diurnal semiarcs are the ascendant to the MC, and the MC to the descendant. The nocturnal semiarcs are the descendant to the IC, and the IC to the ascendant. Time systems take the length of time for some specific point (which depends on the particular house system) to move between two angles: through a semiarc, and then divides this time into three equal parts to give two intermediate times. These two times are used to calculate the intermediate house cusps. The explanation may seem a little complicated, but specific examples, for each house system, should make the ideas clear.

Alcabitius House System

This is the earliest of the time systems of house division, named after the 10th century Arabic astrologer Alcabitius who wrote about the system (although the method was known from the fifth century and possible earlier). Alcabitius houses were popular in Europe until the introduction of the Regiomontanus system in the late 15th century. It is conceptually straightforward and the cusps are easy to calculate.

Consider the point on the ecliptic that is the natal ascendant. As the earth rotates this point will rise until it is the MC. This time is the semiarc of the ascendant: the time for the cusp of the first house to become the MC, the cusp of the tenth house. This time can be trisected: divided into three equal parts. Technically, this is described as trisecting the semiarc of the ascendant.

At the end of the first third of the semiarc time, a particular point in the natal chart will have moved to become the MC. This point is the Alcabitius natal eleventh cusp. Similarly, at the end of two thirds of the period, a different point in the natal chart will have moved to become the MC. This point is the Alcabitius natal twelfth cusp. Finally, in the whole period, a point in the natal chart will have become the MC; this is the Alcabitius first cusp: the ascendant.

Alcabitius Example

Consider the chart shown as figure 10 set for 1 December 2013 at 13:00:00 in London (51N30, 0W10) with Alcabitius cusps.

The ascendant is 19PI00 at 13:00:00 and this position will be the MC at 18:37:07.

The time for the ascendant to become the MC is 5h 37m 7s.

Dividing 5h 37m 7s by three gives 1h 52m 22s, so the intermediate times are 13h 0m 0s + 1h 52m 22s = 14h 52m 22s and 13h 0m + 1h 52m 22s + 1h 52m 22s = 16h 44m 44s.

Finally, calculating the MC for 14:52:22 and 16:44:44 gives 21CP47 and 19AQ18, which are the twelfth and eleventh Alcabitius cusps shown in figure 10.

The second and third cusps are found in the same way but using the IC to Ascendant semiarc. We look back rather than forward and find when the natal ascendant position (19PI00) was the IC. This was at 6:39:04, which was 6h 21m ago (approximately). Dividing this by three gives 2h 7m, so we have 13h 00m – 2h 7m = 10h 53m and 13h 00m – 4h 14m = 8h 46m as the two times of interest. We now find the position of the IC (not the MC as we are using the nocturnal semiarc) at these times and get 25TA52 for the third cusp and 23AR28 for the second cusp, as shown in figure 10.

One advantage of Alcabitius houses is that there is little distortion in the relative sizes of the houses. Although some houses are greater than 30 degrees wide and some less, there are no very wide or very narrow houses, something that happens in some other house systems. Using Campanus houses for example, a chart can have some houses 80 degrees wide and others 10 degrees wide, even at the latitude of London. The modern neglect of the Alcabitius system is somewhat surprising. Perhaps it is time for some research into the usefulness of Alcabitius houses, particularly into transits to the house cusps and their accuracy in timing life events.

Placidus House System

The Placidus system is undoubtedly the most widely used house system in modern practice; however, it can be rather difficult to grasp at first. It is named after the 17th century mathematician Placidus de Tito but seems to have been known in the early 14th century, and possibly earlier. Its popularity may be due to the inclusion of Placidus tables in Raphael's Ephemeris, the standard reference for generations of astrologers in the 19th and 20th centuries. Other house tables were quite uncommon. Placidus claimed that this system matches Ptolemy's rather obscure explanation of houses in the Tetrabiblos.

The calculation of the cusps starts in the same way as Alcabitius: the time for a given position on the ecliptic to move from being the ascendant to being the MC is noted and this time trisected. The calculation then differs from Alcabitius. These intermediate times are the times at which the given ecliptic position will become the eleventh and twelfth house cusps. Note the important difference; we do not calculate the position of the cusps for the time of the natal chart. We calculate the time of a chart in which the given position will be the relevant cusp.

To calculate the position of these intermediate cusps in the natal chart, we need to find the time of an earlier chart whose ascendant position will become the relevant cusp at the time of the natal chart. If this sounds complicated, an example should help.

Placidus Example

Figure 11 is the same chart we used for Alcabitius, but shown with Placidus cusps. We know from the Alcabitius calculations above that the times from the trisection of the ascendant-MC semiarc are 14h 52m 22s and 16h 44m 44s. So, at 14:52:22 the Placidus twelfth cusp will be 19PI00 (the ascendant in figure 11). Similarly, the eleventh Placidus cusp at 16:44:44 will be 19PI00.

As is probably becoming clear, the calculation of Placidus cusps for a natal chart is not straightforward. To find the twelfth cusp, for example, we have to find the time of an earlier chart such that the ascendant of that earlier chart will be the twelfth cusp of the natal chart at the time of the natal chart. The only way to do this is by iteration: trial and error. For the earlier chart, we find the ascendant-MC semiarc time and calculate one third of this. We add that to the time of this earlier chart, and see if the time is equal to the natal time. If it is equal, then the ascendant of the earlier chart becomes the natal twelfth cusp. If the time of the earlier chart plus the trisected semiarc time is after the natal chart time, we need to move the earlier chart back in time and try again; and if the time of the earlier chart plus the trisected semiarc time is before the natal chart time, we need to move the earlier chart forward in time and try again.

Fortunately, tables of houses and computer software do all this for us, but the idea is not simple.

The calculation of the other cusps (second and third) is similar to the Alcabitius calculation: instead of the ascendant-MC semiarc, we use the IC-ascendant semiarc.

There is another way we can think about Placidus cusps that helps understand the idea behind the system. We start by thinking about the time a specific point on the ecliptic takes to get from its rising as the ascendant to its culmination as the MC. This time can be divided into three. For the first third of the time from ascendant to MC, the point is in the twelfth house. For the second third of the time, it is in the eleventh house, and in the last third of the time, it is passing through the tenth house.

Obviously if a planet is not exactly on the ecliptic: if it has celestial latitude, it will rise north or south of the ecliptic's rising position. The time it takes from rising to culmination will be less (north) or more (south) than that of the ecliptic. This will change the house cusp positions. I will consider this latitude problem later.

Koch House System

This is sometimes called the Birthplace house system and is a very recent development. Tables of Koch houses were not published until 1971.

The Koch system is a variant of Alcabitius. To calculate the Alcabitius cusps we used the semiarc of the ascendant (how long it would take for the chart ascendant to become the MC). For Koch we start with the semiarc of the MC: working back from the chart's time to an earlier time when the chart's MC was the ascendant. We trisect this in the usual way and take the ascendants for these times as the house cusps. The easiest way to understand this is by an example of the calculation, which is very simple.

In figure 12, the MC is 25SG45 at 13:00:00. We find the semiarc time by noting that 25SG45 was the ascendant at 09:12:11, so the MC semiarc is 13h 0m 00s – 9h 12m 11s = 3h 47m 49s. We divide this by three to give 1h 15m 56s.

At 9h 12m 11s + 1h 15m 56s = 10h 28m 07s, the ascendant is 14CP25 this is equal to the eleventh cusp shown below.

At 10h 28m 07s + 1h 15m 56s = 11h 44m 03s the ascendant is 10AQ18, equal to the twelfth cusp shown below.

It is worth noting that the difference between the positions of the Koch and Placidus cusps is often not very great, particularly when compared to some space systems, such as Campanus, that can produce very unequal house sizes on the ecliptic.

In many ways, the Koch system is the simplest to calculate, although it does fail in polar latitudes as there can be points on the ecliptic that never rise/set, and so cannot be the ascendant.

Topocentric House System

This is the final system I will consider. It is another recent development, first published in 1961 by Wendel Polich and Nelson Page and is a refinement of the Placidus system. The Topocentric house cusps are usually within a degree or two (depending on geographic latitude) of the Placidus cusps. Polich and Page claim that Topocentric house cusps provide more accurate predictions for the timing of events, using primary directions, than other house systems.

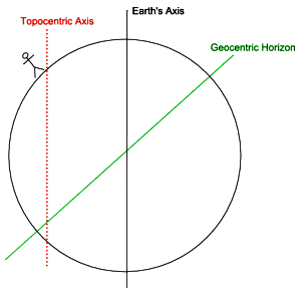
To get a feel for what the Topocentric house system is about, consider the Earth, turning on its axis as shown in Figure 13. To an observer everything in the sky appears to turn about an axis passing through the observer and parallel to the Earth's axis. This axis is called the Topocentric axis. Topocentric means relative to (or centred on) a point on the surface of the Earth.

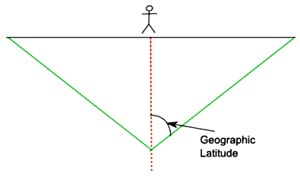
The Geocentric Horizon passes through the centre of the Earth, and is the horizon normally used in astrology. If we rotate the geocentric horizon about the Topocentric axis, we get a cone of rotation, as shown in figure 14. It is this cone that is used to construct the Topocentric house cusps.

The final stage is to take the circular top of this cone and mark-off lines from the centre to the edge at every 30 degrees of rotation. Figure 15 shows this, but only for half the circle to make the diagram manageable and less cluttered. We then trisect these radius lines: the first at the outer edge of the cone, the next one third of the way in, the next two thirds in, and the fourth at the centre of the cone's base. We then move out again. Figure 15 shows the position of these divisions (the length of the arrowed lines is not relevant).

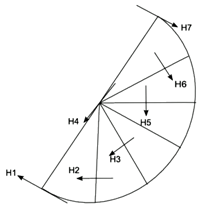
Having found the positions on the radius lines that trisect the cone's radius, we draw lines at right angles to the radius lines, as shown by the arrowed lines. Where these lines intersect the ecliptic are the house cusps (as indicated).

The mathematical calculations of the cusp positions is more complicated than for the other system I have considered in this article, and a full explanation would involve more mathematics than is appropriate here. For a detailed explanation, see Section 4 in Chapter 4 of Holden [6], or the 1964 article in Spica [11] by the developers of the system.

To summarise, the main things to note about the Topocentric House system are that the cusps are very close to the Placidus cusps, the method of construction is based on the horizon as seen from the surface of the earth rather that the geocentric horizon, and that the cusps are claimed to give better timing of events (using primary directions) than other house systems.

A Problem with House Division

There is a potential problem with methods of house division that needs to be considered: planetary latitude. It is only occasionally that a body (apart from the Sun) is exactly on the ecliptic, usually planets have celestial latitude. For Ecliptic house systems: Whole Sign, Equal House and Porphyry, planetary latitude presents no problem as the houses are defined by division of the ecliptic and a planet's ecliptic position is all that matters. However, if the houses are defined not by division of the ecliptic, but by division of some other great circle, then a planet's bodily position may be in a different house to its ecliptic position. This is shown in figure 16 where the planet itself is on the twelfth house side of a house cusp line but its ecliptic longitude is on the eleventh house side. For this illustration I have used a house system that projects from the pole of the equator.

If a house system divides some great circle (such as the equator) and projects these divisions onto the ecliptic from the pole of a circle other than the ecliptic, then the dividing lines between the houses will not intersect the ecliptic at right angles. As in figure 16 the projection is from the pole of the equator, the house dividing lines are at right angles to the equator, but the planet's body is on one side of the line and its ecliptic position is on the other side. This problem is particularly likely to occur when the planet's ecliptic longitude is close to a house cusp. Of the space systems I have discussed, only Morinus projects from the pole of the ecliptic, and so this is the only space system that does not have this latitude problem.

As the conceptual basis of the space systems is to equally divide the space of the celestial sphere, whatever falls within the space of a particular house should be considered as being in that house. The problem of planetary latitude cannot be avoided with these systems. However, this assumes that it is the planet's bodily position that matters. A significant number of astrologers argue that it is not the physical position of a planet that matters but rather its ecliptic position, and so planetary latitude is not relevant. In other words, our astrology is based on ecliptic positions, so a planet's house should also be determined by ecliptic position.

For further discussion of planetary latitude, refer to my article on the Urania Trust website: Charts are not flat

The Time systems of house division also have a latitude problem. When discussing the Alcabitus and Placidus systems, I have talked about the semiarc of a point on the ecliptic. If a planet is not on the ecliptic then its bodily rising will be earlier or later than that of its ecliptic position, and so its semiarc will be longer of shorter. The house cusps will be in different positions on the ecliptic for different planetary latitudes. Note, this is different to the problem with space systems where the ecliptic position of the cusp is the same for all latitudes, but the planet's body may be in a different house: on the other side of a house boundary to its ecliptic position.

The Koch system also has a planetary latitude problem. First, we calculate the MC semiarc, but the time at which a planet's ecliptic longitude was the ascendant and the time the body itself was rising are different. In addition, given the two times from dividing the MC semiarc, we then calculate the ecliptic position rising for these times. The usual problem occurs: the planet does not rise when its ecliptic position rises if the planet has latitude.

In summary, if a planet has latitude then all the space systems except Morinus, and all the time systems have a problem defining a planet's house position as it is not exactly on the ecliptic.

Conclusion

There is still no agreement on the 'correct' system of house division. Even if we accept the suggestion that different systems might be appropriate for different purposes, there is still no agreement on what they are. Many astrologers use either the method of house division they were first taught, or the default method of their computer software, without thinking too hard about the relative strengths and weaknesses of the various systems. I hope this description of the main methods that have been used to construct the houses will help astrologers make considered decisions about which method to use.

Notes and Bibliography

Author: Graham Bates

Graham Bates is co-author of Money and the Markets: An Astrological Guide, along with Jane Chrzanowska Bowles.